GEOMETRIA ANALÍTICA
Considere o ponto A(1,2,1) e o vetor v =(3,1,4) que determinam a reta r. As equações simétricas e reduzidas da reta r estão representadas, respectivamente, na alternativa
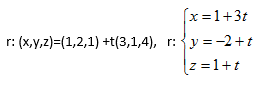

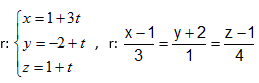
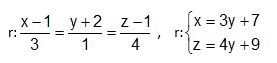
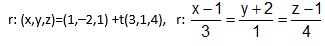
Considere os vetores a=(1,-1,1) e b=(2,-3,4). Um vetor que seja ortogonal tanto ao vetor a quanto ao vetor b está corretamente representado na alternativa
(-1,-2,-1)
(-1,-2,-5)
(-5,-2,1)
(-1,2,1)
(1,-2,-1)
Dados os vetores u=(1,–t,–3),v =(t+3,4–t,1)e w=(t,–2,7). O valor de t para que se tenha a igualdade u.v = (u+v).w é
4
6
-3
2
-1
Qual é o vetor x na igualdade 3x + 2u = (1/2)v + x, sendo dados u = (3, -1) e v = (-2 , 4).
%7D)
%7D)
%7D)
%7D)
%7D)
Um professor de matemática disse a seus alunos que o triângulo ABC da figura representava um terreno e que a parábola é a representação da função f(x) = x2 6x 7.
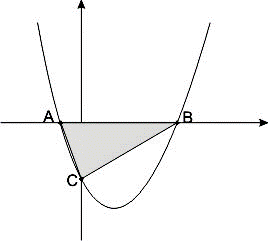
Ele, então, pediu para seus alunos calcularem a área do terreno, em unidades de área (u.a.). Sabendo que os pontos A, B e C são os interceptos dos eixos ordenados, a área do terreno é igual a:
49 u.a.
56 u.a.
42 u.a.
28 u.a.
24,5 u.a.
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio é igual a 2 cm e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(2, – 5) e B(– 2, – 3).
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
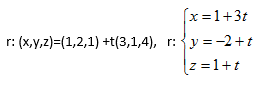

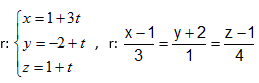
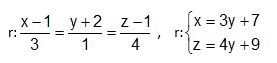
![]()
Considere os vetores a=(1,-1,1) e b=(2,-3,4). Um vetor que seja ortogonal tanto ao vetor a quanto ao vetor b está corretamente representado na alternativa
(-1,-2,-1)
(-1,-2,-5)
(-5,-2,1)
(-1,2,1)
(1,-2,-1)
Dados os vetores u=(1,–t,–3),v =(t+3,4–t,1)e w=(t,–2,7). O valor de t para que se tenha a igualdade u.v = (u+v).w é
4
6
-3
2
-1
Qual é o vetor x na igualdade 3x + 2u = (1/2)v + x, sendo dados u = (3, -1) e v = (-2 , 4).
%7D)
%7D)
%7D)
%7D)
%7D)
Um professor de matemática disse a seus alunos que o triângulo ABC da figura representava um terreno e que a parábola é a representação da função f(x) = x2 6x 7.

Ele, então, pediu para seus alunos calcularem a área do terreno, em unidades de área (u.a.). Sabendo que os pontos A, B e C são os interceptos dos eixos ordenados, a área do terreno é igual a:
49 u.a.
56 u.a.
42 u.a.
28 u.a.
24,5 u.a.
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio é igual a 2 cm e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(2, – 5) e B(– 2, – 3).
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
(-1,-2,-1)
(-1,-2,-5)
(-5,-2,1)
(-1,2,1)
(1,-2,-1)
Dados os vetores u=(1,–t,–3),v =(t+3,4–t,1)e w=(t,–2,7). O valor de t para que se tenha a igualdade u.v = (u+v).w é
4
6
-3
2
-1
Qual é o vetor x na igualdade 3x + 2u = (1/2)v + x, sendo dados u = (3, -1) e v = (-2 , 4).
%7D)
%7D)
%7D)
%7D)
%7D)
Um professor de matemática disse a seus alunos que o triângulo ABC da figura representava um terreno e que a parábola é a representação da função f(x) = x2 6x 7.

Ele, então, pediu para seus alunos calcularem a área do terreno, em unidades de área (u.a.). Sabendo que os pontos A, B e C são os interceptos dos eixos ordenados, a área do terreno é igual a:
49 u.a.
56 u.a.
42 u.a.
28 u.a.
24,5 u.a.
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio é igual a 2 cm e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(2, – 5) e B(– 2, – 3).
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
4
6
-3
2
-1
Qual é o vetor x na igualdade 3x + 2u = (1/2)v + x, sendo dados u = (3, -1) e v = (-2 , 4).
%7D)
%7D)
%7D)
%7D)
%7D)
Um professor de matemática disse a seus alunos que o triângulo ABC da figura representava um terreno e que a parábola é a representação da função f(x) = x2 6x 7.

Ele, então, pediu para seus alunos calcularem a área do terreno, em unidades de área (u.a.). Sabendo que os pontos A, B e C são os interceptos dos eixos ordenados, a área do terreno é igual a:
49 u.a.
56 u.a.
42 u.a.
28 u.a.
24,5 u.a.
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio é igual a 2 cm e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(2, – 5) e B(– 2, – 3).
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
Um professor de matemática disse a seus alunos que o triângulo ABC da figura representava um terreno e que a parábola é a representação da função f(x) = x2 6x 7.

Ele, então, pediu para seus alunos calcularem a área do terreno, em unidades de área (u.a.). Sabendo que os pontos A, B e C são os interceptos dos eixos ordenados, a área do terreno é igual a:
49 u.a.
56 u.a.
42 u.a.
28 u.a.
24,5 u.a.
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio é igual a 2 cm e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(2, – 5) e B(– 2, – 3).
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.

49 u.a.
56 u.a.
42 u.a.
28 u.a.
24,5 u.a.
Assinale a alternativa que corresponde à equação reduzida da circunferência cujo raio é igual a 2 cm e o seu centro coincide com o ponto médio do segmento de extremidades A e B, sendo A(2, – 5) e B(– 2, – 3).
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
(x + 1)² + (y – 4)² = 10
x² + (y + 4)² = 4
(x+2)² + (y + 4)² = 4
x² + y² + 6x + 10y = 15
x² + y² + 2x – 2y – 3 = 0
Encontre o foco e uma equação da diretriz para a parábola x2 = 8y.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
F(0, 1/2) e y = 0
F(0, 2) e y = -2
F(2, 1/2) e y = 2
F(-1/2, 0) e y = 1/2
F(2, 0) e y = 2
Determine o valor de m para que seja de 30° o ângulo entre os planos:

m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine para que valores de m e n o ponto F(m, 5, n) pertence a r.
m = -1 ou 7
m = 5
m = 1 ou -7
m = 2
m = 1 ou 7